Research
The Out Of Equilibrium Group @ UML is interested in superstatistics, randomness, machine learning, topology, algorithm development, adiabatic statistical ensembles, and active matter.
Here are some themes and techniques that we currently work on:
Superstatistics. Superstatistics is a combination of two different statistics related to driven nonequilibrium systems with a stationary state and intensive parameter fluctuations. It includes Tsallis statistics as a special case.
Generative Machine Learning. Boltzmann Machine is a generative unsupervised model.
Combining AI/ML methods and fluorescence polarization approach for cancer diagnosis. In collaboration with the Yaroslavsky’s group, we develop theoretical frameworks, new physics-informed machine learning, and artificial intelligence algorithms for biomedical optical imaging and novel image-guided intervention techniques in cancer research
Control Strategies for Open Quantum Dynamics - A Combined Deep learning Theoretical Physics Approach. The goal of this project is to create strategies that can control correlated noise to perform quantum operations like single and two-qubit gates. It’s essential to understand how the environment affects an out-of-equilibrium quantum system to build a fault-tolerant quantum computer and develop high-sensitivity sensors. This is done in collaboration with the Ribeiro’s group.
Quantum-enhanced Monte Carlo simulations. In the future, quantum computers could provide faster solutions for sampling problems than classical computers. Developing and testing new quantum algorithms could lead to significant speedup and solve bottleneck issues in machine learning, statistical physics, and optimization problems.
Active matter assemble into reconfigurable nonequilibrium structures. 
With the MSNEP group, we investigate how active fluids respond to spatial light patterns through simulations and experiments on light-activated self-propelled colloidal particles.
Active matter and colored noise. The study of the motion of small particles suspended in a fluid ad moving under the influence of random forces resulting from collisions with fluid molecules induced by thermal fluctuations is known as Browninan motion. The thermal fluctuations occur on a much shorter timescale than that of the Brownian particle. Therefore, it is a good approximation to assume that the random forces are delta functions that are uncorrelated, as perceived by the particle on its own, much slower time scale. However in reality, this is never exactly the case.
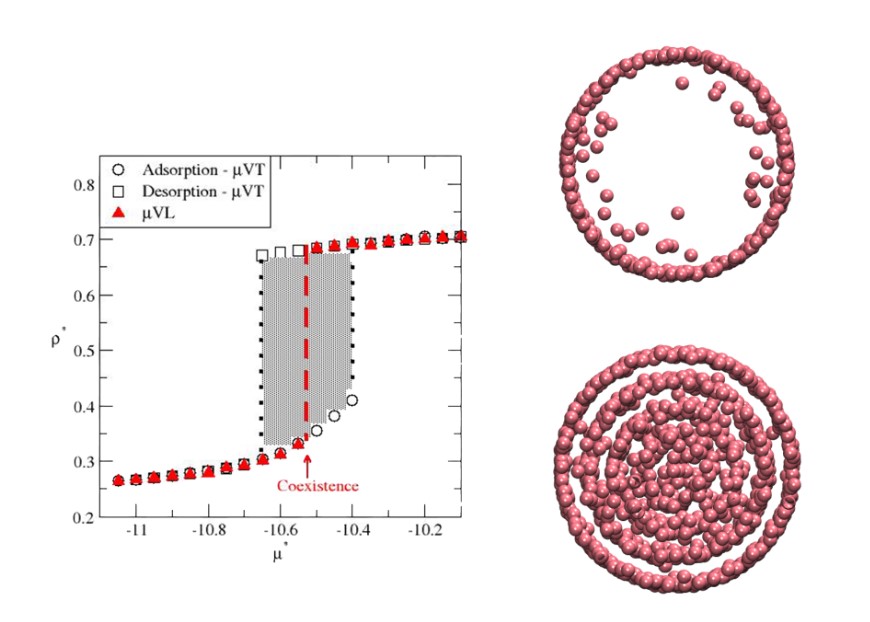
The central role of entropy in adiabatic ensembles. Using the principles of statistical mechanics and thermodynamics, we can define eight different ensembles. In addition to the Guggenheim ensemble (the “fifth” statistical ensemble), one can modify the thermodynamic constratints to define three additional statistical ensembles. Brown, Hill, and Ray developed the isoenthalpic-isobaric ensemble (N,P,H), the grand-isochoric adaibatic ensemble (\mu,V,L) ensemble, and the grand-isobaric adiabatic ensemble (\mu,P,R) ensemble, using the Legendre-Laplace mapping procedure. Together with the microcanonical ensemble, they form a set of 4 adiabatic ensembles in which the value of a heat function os constant rather than the temperature.
